निर्देश (1 – 5): निम्नलिखित जानकारी को ध्यान से पढ़ें और दिए गए प्रश्नों के उत्तर दें।
दो दोस्त A और B हैं, जो अलग-अलग गेम खेल रहे हैं जिसमें पासा और कार्ड शामिल हैं। पांच प्रकार के गेम (यानी) गेम 1, गेम 2, गेम 3, गेम 4 और गेम 5 हैं। गेम 1 में, दोनों को वैकल्पिक रूप से पासा फेंकने की अनुमति है। यदि फेंकने पर 5 से अधिक आता हैं, तो व्यक्ति को विजेता कहा जाता है। गेम 2 में, वे वैकल्पिक रूप से पासा की एक जोड़ी फेंकते हैं।
A जीतता है यदि उसे B को 10 का योग मिलने से पहले 9 का योग मिलता है और B जीतता है यदि उसे A को 9 का योग मिलने से पहले 10 का योग मिलता है। गेम 3 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने की अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक संख्या कार्ड फेंकता है। गेम 4 में, दोनों को वैकल्पिक रूप से पासा की एक जोड़ी को फेंकने की अनुमति है। A जीतता है यदि उसे B को 8 का गुणज मिलने से पहले 6 का गुणज मिलता है और B जीतता है यदि उसे A को 6 का गुणज मिलने से पहले 8 का गुणज मिलता है।गेम 5 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक अक्षर कार्ड फेंकता है।1) यदि B गेम 4 शुरू करता है, तो अपने तीसरे प्रयास में B की जीत की संभावना ज्ञात करें।
a) 225/5832
b) 321/5832
c) 289/5832
d) 361/5832
e) इनमे से कोई नहीं
1) Answer: c)
अभिप्रायोगो की कुल संख्या = 62 = 36

6 के गुणज मिलने की कुल संभावनाएं= (1,6), (2,3), (3,2), (6,1) = 4
8 के गुणज मिलने की कुल संभावनाएं= (2,4), (4,2)
A की जीतने की संभावना = 4/36 = 1/9
A की हारने की संभावना = (36-4) / 36 = 32/36 = 8/9
B की जीतने की संभावना = 2/36 = 1/18
B की हारने की संभावना = (36-2) / 36
= 34/36 = 17/18
अपने तीसरे प्रयास में B के जीतने की संभावना
= 17/18*17/18*1/18
= 289/5832
निर्देश (1 – 5): निम्नलिखित जानकारी को ध्यान से पढ़ें और दिए गए प्रश्नों के उत्तर दें।
दो दोस्त A और B हैं, जो अलग-अलग गेम खेल रहे हैं जिसमें पासा और कार्ड शामिल हैं। पांच प्रकार के गेम (यानी) गेम 1, गेम 2, गेम 3, गेम 4 और गेम 5 हैं। गेम 1 में, दोनों को वैकल्पिक रूप से पासा फेंकने की अनुमति है। यदि फेंकने पर 5 से अधिक आता हैं, तो व्यक्ति को विजेता कहा जाता है। गेम 2 में, वे वैकल्पिक रूप से पासा की एक जोड़ी फेंकते हैं। A जीतता है यदि उसे B को 10 का योग मिलने से पहले 9 का योग मिलता है और B जीतता है यदि उसे A को 9 का योग मिलने से पहले 10 का योग मिलता है। गेम 3 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने की अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक संख्या कार्ड फेंकता है। गेम 4 में, दोनों को वैकल्पिक रूप से पासा की एक जोड़ी को फेंकने की अनुमति है। A जीतता है यदि उसे B को 8 का गुणज मिलने से पहले 6 का गुणज मिलता है और B जीतता है यदि उसे A को 6 का गुणज मिलने से पहले 8 का गुणज मिलता है।गेम 5 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक अक्षर कार्ड फेंकता है।
2) यदि A गेम 2 शुरू करता है, तो अपने दूसरे प्रयास में A के जीतने की संभावना ज्ञात करें।
a) 7/81
b) 8/81
c) 11/81
d) 13/81
e) 19/81
2) Answer: b)
अभिप्रायोगो की कुल संख्या= 62 = 36

9 की योग प्राप्त करने की कुल संभावनाएं= (3,6), (4,5), (5,4), (6,3) = 4
10 की योग प्राप्त करने की कुल संभावनाएं= (4,6), (5,5), (6,4) = 3
A की जीतने की संभावना = 4/36 = 1/9
A की हारने की संभावना = 1 – 1/9 = 8/9
B की जीतने की संभावना = 3/36 = 1/12
B की हारने की संभावना = 1 – 1/12 = 11/12
दूसरे प्रयास में A के जीतने की संभावना
= 8/9*1/9 = 8/81
निर्देश (1 – 5): निम्नलिखित जानकारी को ध्यान से पढ़ें और दिए गए प्रश्नों के उत्तर दें।
दो दोस्त A और B हैं, जो अलग-अलग गेम खेल रहे हैं जिसमें पासा और कार्ड शामिल हैं। पांच प्रकार के गेम (यानी) गेम 1, गेम 2, गेम 3, गेम 4 और गेम 5 हैं। गेम 1 में, दोनों को वैकल्पिक रूप से पासा फेंकने की अनुमति है। यदि फेंकने पर 5 से अधिक आता हैं, तो व्यक्ति को विजेता कहा जाता है। गेम 2 में, वे वैकल्पिक रूप से पासा की एक जोड़ी फेंकते हैं। A जीतता है यदि उसे B को 10 का योग मिलने से पहले 9 का योग मिलता है और B जीतता है यदि उसे A को 9 का योग मिलने से पहले 10 का योग मिलता है। गेम 3 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने की अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक संख्या कार्ड फेंकता है। गेम 4 में, दोनों को वैकल्पिक रूप से पासा की एक जोड़ी को फेंकने की अनुमति है। A जीतता है यदि उसे B को 8 का गुणज मिलने से पहले 6 का गुणज मिलता है और B जीतता है यदि उसे A को 6 का गुणज मिलने से पहले 8 का गुणज मिलता है।गेम 5 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक अक्षर कार्ड फेंकता है।
3) यदि A गेम 1 शुरू करता है, तो अपने तीसरे प्रयास में A के जीतने की संभावना ज्ञात करें।
a) 125/216
b) 25/36
c) 5/216
d) 25/216
e) इनमे से कोई नहीं
3) Answer: d)
अभिप्रायोगो की कुल संख्या = 61 = 6 = (1, 2, 3, 4, 5, 6)
गेम 1 में, दोनों को वैकल्पिक रूप से पासा फेंकने की अनुमति है। यदि फेंकने पर 5 से अधिक आता हैं, तो व्यक्ति को विजेता कहा जाता है।
जीतने की संभावना = 1/6
हारने की संभावना = 5/6
अपने तीसरे प्रयास में A के जीतने की संभावना
= 5/6*5/6*1/6
= 25/216
निर्देश (1 – 5): निम्नलिखित जानकारी को ध्यान से पढ़ें और दिए गए प्रश्नों के उत्तर दें।
दो दोस्त A और B हैं, जो अलग-अलग गेम खेल रहे हैं जिसमें पासा और कार्ड शामिल हैं। पांच प्रकार के गेम (यानी) गेम 1, गेम 2, गेम 3, गेम 4 और गेम 5 हैं। गेम 1 में, दोनों को वैकल्पिक रूप से पासा फेंकने की अनुमति है। यदि फेंकने पर 5 से अधिक आता हैं, तो व्यक्ति को विजेता कहा जाता है। गेम 2 में, वे वैकल्पिक रूप से पासा की एक जोड़ी फेंकते हैं। A जीतता है यदि उसे B को 10 का योग मिलने से पहले 9 का योग मिलता है और B जीतता है यदि उसे A को 9 का योग मिलने से पहले 10 का योग मिलता है। गेम 3 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने की अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक संख्या कार्ड फेंकता है। गेम 4 में, दोनों को वैकल्पिक रूप से पासा की एक जोड़ी को फेंकने की अनुमति है। A जीतता है यदि उसे B को 8 का गुणज मिलने से पहले 6 का गुणज मिलता है और B जीतता है यदि उसे A को 6 का गुणज मिलने से पहले 8 का गुणज मिलता है।गेम 5 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक अक्षर कार्ड फेंकता है।
4) यदि A गेम 3 शुरू करता है, तो अपने तीसरे प्रयास में A के जीतने की संभावना ज्ञात करें।
a) 196/2197
b) 154/2197
c) 121/2197
d) 144/2197
e) इनमे से कोई नहीं
4) Answer: d)
कुल कार्ड = 52
कुल संख्या कार्ड = 9 * 4 = 36
कुल मुख कार्ड = 3 * 4 = 12
कुल अक्षर कार्ड = 4 * 4 = 16
A की जीतने की संभावना = 36/52
= 9/13
A की हारने की संभावना = (52-36) / 52
= 16/52 = 4/13
तीसरे प्रयास में A के जीत की संभावना
= 4/13*4/13*9/13
=144/2197
निर्देश (1 – 5): निम्नलिखित जानकारी को ध्यान से पढ़ें और दिए गए प्रश्नों के उत्तर दें।
दो दोस्त A और B हैं, जो अलग-अलग गेम खेल रहे हैं जिसमें पासा और कार्ड शामिल हैं। पांच प्रकार के गेम (यानी) गेम 1, गेम 2, गेम 3, गेम 4 और गेम 5 हैं। गेम 1 में, दोनों को वैकल्पिक रूप से पासा फेंकने की अनुमति है। यदि फेंकने पर 5 से अधिक आता हैं, तो व्यक्ति को विजेता कहा जाता है। गेम 2 में, वे वैकल्पिक रूप से पासा की एक जोड़ी फेंकते हैं। A जीतता है यदि उसे B को 10 का योग मिलने से पहले 9 का योग मिलता है और B जीतता है यदि उसे A को 9 का योग मिलने से पहले 10 का योग मिलता है। गेम 3 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने की अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक संख्या कार्ड फेंकता है। गेम 4 में, दोनों को वैकल्पिक रूप से पासा की एक जोड़ी को फेंकने की अनुमति है। A जीतता है यदि उसे B को 8 का गुणज मिलने से पहले 6 का गुणज मिलता है और B जीतता है यदि उसे A को 6 का गुणज मिलने से पहले 8 का गुणज मिलता है।गेम 5 में दोनों को प्रतिस्थापन के बिना 52 कार्ड के अच्छी तरह से फेरबदल की हुई कार्ड की गड्डी से एक कार्ड फेंकने अनुमति है। किसी भी व्यक्ति को इस गेम का विजेता कहा जाता है, यदि वह एक अक्षर कार्ड फेंकता है।
5) यदि A गेम 5 शुरू करता है, तो अपने तीसरे प्रयास में A के जीतने की संभावना ज्ञात करें।
a) 216/2197
b) 288/2197
c) 252/2197
d) 361/2197
e) इनमे से कोई नहीं
5) Answer: e)
कुल कार्ड = 52
कुल संख्या कार्ड = 9 * 4 = 36
कुल मुख कार्ड = 3 * 4 = 12
कुल अक्षर कार्ड = 4 * 4 = 16
A के जीतने की संभावना = 16/52
= 4/13
A के हारने की संभावना = 1 – 4/13
= 9/13
अपने तीसरे प्रयास में A के जीतने की संभावना
= 9/13 * 9/13 * 4/13
= 324/2197
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
विभिन्न विभाग में एक कार्यालय में कर्मचारियों की संख्या लाइन ग्राफ में दर्शाई गई है।
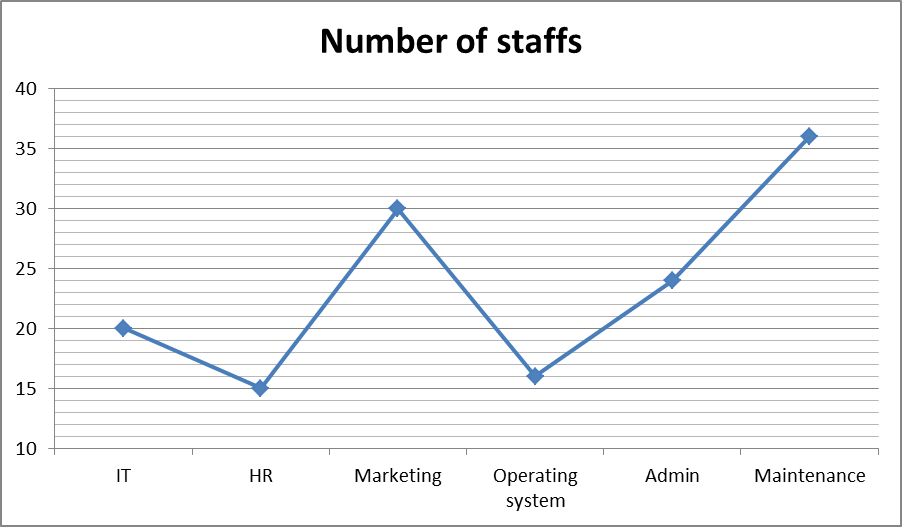
6) किसी प्रोजेक्ट के लिए IT, HR और एडमिन डिपार्टमेंट सदस्य के 5 सदस्यों की एक टीम बनाई जानी है, टीम के गठन के तरीकों की संख्या ज्ञात करें, यदि टीम में एडमिन डिपार्टमेंट को छोड़कर एक ही डिपार्टमेंट के 2 सदस्य नहीं हैं?
a) 652050
b) 687900
c) 989820
d) 607200
e) इनमे से कोई नहीं
6) Answer: d)
तरीकों की संख्या = 20C1*15C1*24C3
= 20*15*(24*23*22/1*2*3)
= 607200
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
विभिन्न विभाग में एक कार्यालय में कर्मचारियों की संख्या लाइन ग्राफ में दर्शाई गई है।

7) कितने तरीकों से, 4 सदस्यों की एक टीम बनाई जा सकती है ताकि टीम में दो विशेष आईटी कर्मचारी हमेशा रहें?
a) 6870
b) 6980
c) 7290
d) 9870
e) इनमे से कोई नहीं
7) Answer: d)
तरीकों की संख्या = (20+15+30+16+24+36)C(4 – 2)
= 141C2
= (141*140)/(1*2)
= 9870
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
विभिन्न विभाग में एक कार्यालय में कर्मचारियों की संख्या लाइन ग्राफ में दर्शाई गई है।

8) 5 सदस्यों की एक टीम आईटी और मार्केटिंग स्टाफ के साथ बनाई जानी है। ऐसा करने के तरीकों की संख्या ज्ञात करें ताकि टीम में प्रत्येक विभाग का कम से कम 1 सदस्य है?
a) 1879500
b) 1988820
c) 1960750
d) 2168910
e) इनमे से कोई नहीं
8) Answer: c)
आवश्यक संभावना
= (20C1*30C4 + 20C2*30C3 + 20C3*30C2 + 20C4*30C1)
= [(20*(30*29*28*27/1*2*3*4)) + ((20*19/1*2)*(30*29*28/1*2*3)) + ((20*19*18/1*2*3)*(30*29/1*2)) + ((20*19*18*17/1*2*3*4)*30)
= (25*29*28*27) + (190*5*29*28) + (20*19*3*15*29) + (5*19*3*17*30)
= 548100 + 771400 + 495900 + 145350
= 1960750
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
विभिन्न विभाग में एक कार्यालय में कर्मचारियों की संख्या लाइन ग्राफ में दर्शाई गई है।

9) एक परियोजना के लिए 5 सदस्यों की एक टीम बनाई जानी है, ताकि टीम के पास ऑपरेटिंग सिस्टम को छोड़कर प्रत्येक विभाग का कम से कम एक सदस्य हो। इसे कितने तरीकों से किया जा सकता है?
a) 7776000
b) 7767000
c) 8977000
d) 8979400
e) 6988900
9) Answer: a)
तरीकों की संख्या = 20C1*15C1*30C1*24C1*36C1
= 20*15*30*24*36
= 77760000
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
विभिन्न विभाग में एक कार्यालय में कर्मचारियों की संख्या लाइन ग्राफ में दर्शाई गई है।

10) यदि 6 एडमिन डिपार्टमेंट के कर्मचारी और 6 ऑपरेटिंग सिस्टम विभाग के कर्मचारियों को सीटों की एक पंक्ति (नंबर 1 – 12) में बैठाया जाना है, तो कितने तरीकों से उन्हें बैठाया जा सकता है यदि एडमिन डिपार्टमेंट के कर्मचारी केवल सम संख्या वाली सीटों पर बैठते हैं ?
a) 1440
b) 5040
c) 1296
d) 720
e) इनमे से कोई नहीं
10) Answer: e)
तरीकों की संख्या = 6! * 6!
= 6*5*4*3*2*1 * 6*5*4*3*2*1
= 720*720
= 518400

