निर्देश (1 – 5): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और नीचे दिए गए प्रश्नों के उत्तर दें:
निम्न पाई चार्ट पांच छात्रों द्वारा पूरा किए गए कार्य के भाग के प्रतिशत वार वितरण का निरूपण करता है।
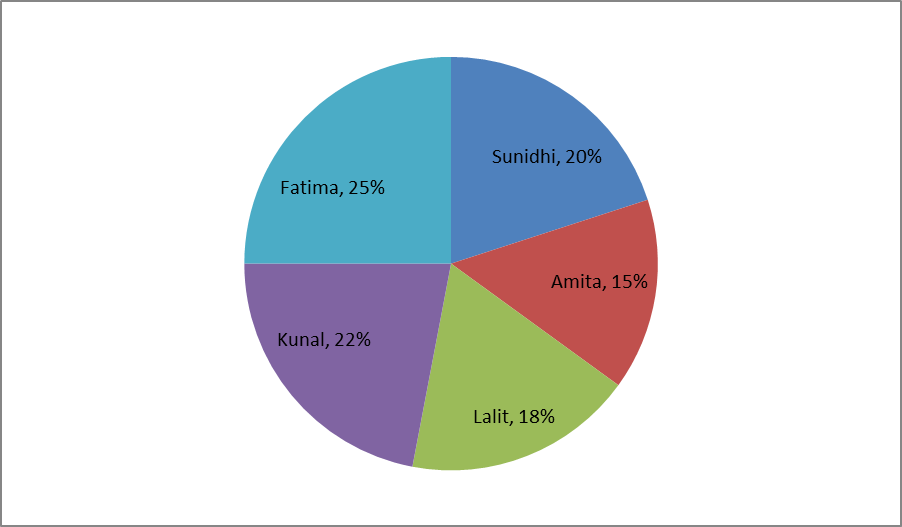
निम्नलिखित लाइन ग्राफ उनके काम के हिस्से को पूरा करने के लिए उनके द्वारा लिए गए दिनों की संख्या को दर्शाता है।
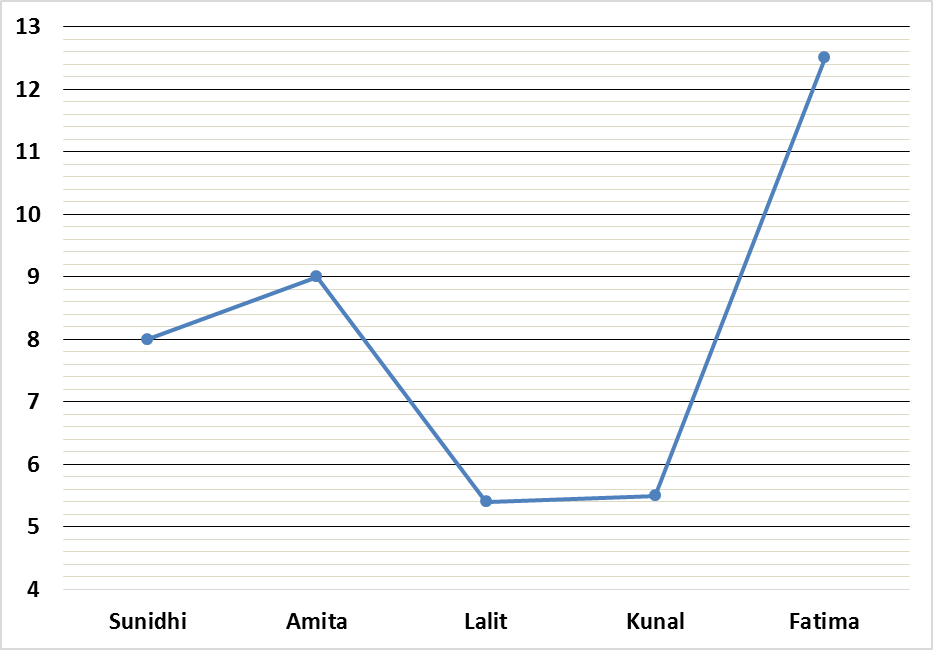
1) ललित, कुणाल और फातिमा ने काम शुरू किया। ललित ने काम पूरा होने से पांच दिन पहले छोड़ दिया और कुणाल ने काम पूरा होने से दस दिन पहले छोड़ दिया और फातिमा ने काम पूरा होने तक काम किया। कुल दिनों की संख्या ज्ञात कीजिये?
a) 229/7 दिन
b) 231/9 दिन
c) 235/14 दिन
d) 238/5 दिन
e) इनमे से कोई नहीं
1) Answer: c)
ललित 5.4 दिनों में 18% काम कर सकता है
=> ललित 5.4 / 18 दिनों में 1% काम कर सकता है
=> ललित 5.4 / 18 x 100 = 30 दिनों में 100% काम कर सकता है।
कुणाल 5.5 दिनों में 22% काम कर सकता है
=> कुणाल 5.5 / 22 दिनों में 1% कार्य कर सकता है
=> कुणाल 5.5/22 x 100 = 25 दिन में 100% काम कर सकता है।
फातिमा 12.5 दिनों में 25% काम कर सकती है
=> फातिमा 12.5 / 25 दिनों में 1% काम कर सकती है
=> फातिमा 100% काम 12.5 / 25 x 100 = 50 दिन में कर सकती है।
माना कि, काम n दिनों में पूरा किया गया
(n – 5)/30 + (n – 10)/25 + n/50 = 1
=> (5n – 25 + 6n – 60 + 3n)/150 = 1
=> 14n – 85 = 150
=> 14n = 150 + 85
=> 14n = 235
=> n = 235/14 दिन
निर्देश (1 – 5): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और नीचे दिए गए प्रश्नों के उत्तर दें:
निम्न पाई चार्ट पांच छात्रों द्वारा पूरा किए गए कार्य के भाग के प्रतिशत वार वितरण का निरूपण करता है।

निम्नलिखित लाइन ग्राफ उनके काम के हिस्से को पूरा करने के लिए उनके द्वारा लिए गए दिनों की संख्या को दर्शाता है।

2) सुनिधि ने काम शुरू किया। अमिता और ललित, अमिता के साथ शुरू होने वाले वैकल्पिक दिनों में उसके साथ होते हैं यानी पहले दिन सुनिधि और अमिता काम करती है, दूसरे दिन सुनिधि और ललित काम करते हैं और इसी तरह। कार्य कितने दिनों में पूरा होगा?
a) 20 दिन
b) 18 दिन
c) 12 दिन
d) 16 दिन
e) इनमे से कोई नहीं
2) Answer: a)
सुनिधि 8 दिनों में 20% काम कर सकती है
=> सुनिधि 8/20 दिनों में 1% काम कर सकती है
=> सुनिधि 8/20 x 100 = 40 दिनों में 100% काम कर सकती है।
अमिता 9 दिनों में 15% काम कर सकती है
=> अमिता 9/15 दिनों में 1% काम कर सकती है
=> अमिता 100% काम 9/15 x 100 = 60 दिनों में कर सकती है।
ललित 5.4 दिनों में 18% काम कर सकता है
=> ललित 5.4 / 18 दिनों में 1% काम कर सकता है
=> ललित 5.4 / 18 x 100 = 30 दिनों में 100% काम कर सकता है।
2 दिनों में पूरा होने वाले कार्य का हिस्सा = 1/40 + 1/60 + 1/40 + 1/30
= (3 + 2 + 3 + 4) / 120
= 12/120
= 1/10
1/10 कार्य पूरा करने में लगने वाला समय = 2 दिन
=> 1 काम पूरा करने में लगने वाला समय = 2 x 10 = 20 दिन
निर्देश (1 – 5): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और नीचे दिए गए प्रश्नों के उत्तर दें:
निम्न पाई चार्ट पांच छात्रों द्वारा पूरा किए गए कार्य के भाग के प्रतिशत वार वितरण का निरूपण करता है।

निम्नलिखित लाइन ग्राफ उनके काम के हिस्से को पूरा करने के लिए उनके द्वारा लिए गए दिनों की संख्या को दर्शाता है।

3) सरिता की दक्षता, कुणाल की दक्षता से 25% अधिक है। एक साथ सरिता, अमिता और फातिमा द्वारा काम पूरा करने में कितने दिन लगते हैं?
a) 70/12 दिन
b) 150/13 दिन
c) 90/7 दिन
d) 113/5 दिन
e) इनमे से कोई नहीं
3) Answer: b)
कुणाल 5.5 दिनों में 22% काम कर सकता है
=> कुणाल 5.5 / 22 दिनों में 1% कार्य कर सकता है
=> कुणाल 5.5/22 x 100 = 25 दिन में 100% काम कर सकता है।
1 / सरिता = 1/25 x 125/100
=> 1 / सरिता = 1/20
अमिता 9 दिनों में 15% काम कर सकती है
=> अमिता 9/15 दिनों में 1% काम कर सकती है
=> अमिता 100% काम 9/15 x 100 = 60 दिनों में कर सकती है।
फातिमा 12.5 दिनों में 25% काम कर सकती है
=> फातिमा 12.5 / 25 दिनों में 1% काम कर सकती है
=> फातिमा 100% काम 12.5 / 25 x 100 = 50 दिन में कर सकती है।
माना कि आवश्यक दिनों की संख्या = n
n x (1/20 + 1/60 + 1/50) = 1
=>n x (15 + 5 + 6)/300 = 1
=> n = 300/26
=> n = 150/13 दिन
निर्देश (1 – 5): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और नीचे दिए गए प्रश्नों के उत्तर दें:
निम्न पाई चार्ट पांच छात्रों द्वारा पूरा किए गए कार्य के भाग के प्रतिशत वार वितरण का निरूपण करता है।

निम्नलिखित लाइन ग्राफ उनके काम के हिस्से को पूरा करने के लिए उनके द्वारा लिए गए दिनों की संख्या को दर्शाता है।

4) सुनिधि और राकेश ने काम शुरू किया और 20 दिनों के बाद छोड़ दिया। काम के शेष भाग को पूरा करने के लिए निशा द्वारा लिए गए दिनों की संख्या ज्ञात कीजिए।
कथन I: राकेश और निशा एक साथ 300/29 दिनों में एक तिहाई काम पूरा कर सकते हैं।
कथन II: रिषभ अकेले 35 दिनों में काम पूरा कर सकता है। निशा की मदद से वह 315/16 दिनों में काम पूरा कर सकते हैं।
a) केवल कथन I प्रश्न का उत्तर देने के लिए अकेले पर्याप्त है, लेकिन केवल कथन II अकेले पर्याप्त नहीं है।
b) कथन II अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, लेकिन केवल कथन I अकेले ही पर्याप्त नहीं है।
c) या तो कथन I या कथन II अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है।
d) प्रश्न के उत्तर के लिए I और II दोनों कथनों की आवश्यकता है।
e) दोनों कथन I और II एक साथ प्रश्न का उत्तर देने के लिए पर्याप्त नहीं हैं।
4) Answer: d)
सुनिधि 8 दिनों में 20% काम कर सकती है
=> सुनिधि 8/20 दिनों में 1% काम कर सकती है
=> सुनिधि 8/20 x 100 = 40 दिनों में 100% काम कर सकती है।
I से:
300/29 x (1 / राकेश + 1 / निशा) = 1/3
=> 1 / राकेश + 1 / निशा = 1/3 x 29/300
=> 1 / राकेश + 1 / निशा = 29/900
II से:
1 / ऋषभ = 1/35
1 / ऋषभ + 1 / निशा = 16/315
=> 1/35 + 1 / निशा = 16/315
=> 1 / निशा = 16/315 – 1/35
=> 1 / निशा = (16 – 9) / 315
=> 1 / निशा = 7/315
=> 1 / निशा = 1/45
I और II से:
1 / राकेश + 1/45 = 29/900
=> 1 / राकेश = 29/900 – 1/45
=> 1 / राकेश = (29 – 20) / 900
=> 1 / राकेश = 9/900
=> 1 / राकेश = 1/100
माना कि आवश्यक दिनों की संख्या = n
20/40 + 20/100 + n/45 = 1
=> ½ + 1/5 + n/45 = 1
=> n/45 = 1 – ½ – 1/5
=> n/45 = (10 – 5 – 2)/10
=> n = 45 x 3/10
=> n = 27/2 दिन
इसलिए, प्रश्न के उत्तर के लिए I और II दोनों कथनों की आवश्यकता है।
निर्देश (1 – 5): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और नीचे दिए गए प्रश्नों के उत्तर दें:
निम्न पाई चार्ट पांच छात्रों द्वारा पूरा किए गए कार्य के भाग के प्रतिशत वार वितरण का निरूपण करता है।

निम्नलिखित लाइन ग्राफ उनके काम के हिस्से को पूरा करने के लिए उनके द्वारा लिए गए दिनों की संख्या को दर्शाता है।

5) राघव और कुणाल की दक्षता एक साथ. मीना और फातिमा की दक्षता का कितना प्रतिशत है?
कथन I: कुणाल और मीना एक साथ 300/17 दिनों में काम पूरा कर सकते हैं। राघव की मदद से वे 100/9 दिन में काम पूरा कर सकते हैं।
कथन II: राघव की दक्षता मीणा की दक्षता से दोगुनी है।
a) केवल कथन I प्रश्न का उत्तर देने के लिए अकेले पर्याप्त है, लेकिन केवल कथन II अकेले पर्याप्त नहीं है।
b) कथन II अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है, लेकिन केवल कथन I अकेले ही पर्याप्त नहीं है।
c) या तो कथन I या कथन II अकेले प्रश्न का उत्तर देने के लिए पर्याप्त है।
d) प्रश्न के उत्तर के लिए I और II दोनों कथनों की आवश्यकता है।
e) दोनों कथन I और II एक साथ प्रश्न का उत्तर देने के लिए पर्याप्त नहीं हैं।
5) Answer: a)
I से:
कुणाल 5.5 दिनों में 22% काम कर सकता है
=> कुणाल 5.5 / 22 दिनों में 1% कार्य कर सकता है
=> कुणाल 5.5/22 x 100 = 25 दिन में 100% काम कर सकता है।
1 / कुणाल + 1 / मीना = 17/300
=> 1/25 + 1 / मीना = 17/300
=> 1 / मीना = 17/300 – 1/25
=> 1 / मीना = (17 – 12) / 300
=> 1 / मीना = 5/300
=> 1 / मीना = 1/60
1 / कुणाल + 1 / मीना + 1 / राघव = 9/100
=> 1/25 + 1/60 + 1 / राघव = 9/100
=> 1 / राघव = 9/100 – 1/25 – 1/60
=> 1 / राघव = (27 – 12 – 5) / 300
=> 1 / राघव = 10/300
=> 1 / राघव = 1/30
आवश्यक प्रतिशत = [(1/30 + 1/25) / (1/60 + 1/50)] x 100
= [(10 + 12)/300]/[(5 + 6)/300] x 100
= 22/11 x 100
= 200%
कथन II:
1 / राघव = 2 / मीना
इसलिए, केवल कथन I प्रश्न का उत्तर देने के लिए अकेले पर्याप्त है, लेकिन केवल कथन II अकेले पर्याप्त नहीं है।
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
तालिका विभिन्न स्कूलों से विभिन्न कक्षाओं में भाग लेने वाले छात्रों की संख्या को दर्शाता है।
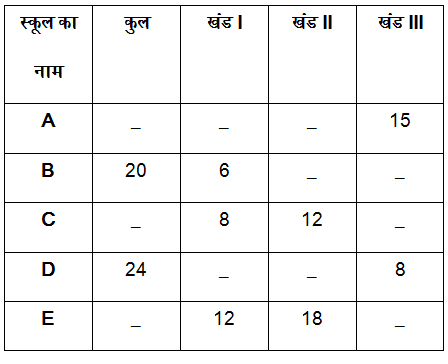
6) चार छात्रों के एक समूह को स्कूल C से बनना है, ताकि समूह में प्रत्येक खंड से एक छात्र शामिल हो और शेष किसी भी खंड से हो। यह संभव हो सकने वाले तरीकों की संख्या 25920 है। स्कूल C से खंड III में छात्रों की संख्या ज्ञात कीजिए?
a) 15
b) 12
c) 10
d) 20
e) 18
6) Answer: c)
स्कूल C से खंड III में छात्रों की संख्या= x
स्कूल C में छात्रों की कुल संख्या= x + 8 + 12 = 20 + x
संभावित तरीकों की संख्या = 8C1 * 12C1 * xC1 * (20 + x – 3) C1 = 25920
8 * 12 * x * (17+x) = 25920
17x + x2 = 270
= > x2 + 17x – 270 = 0
= > x2 – 10x + 27x – 270 = 0
= > x (x – 10) + 27 (x – 10) = 0
= > x = 10, – 27 (ऋणात्मक मान को हटाने पर,)
स्कूल C से खंड III में छात्रों की संख्या = 10
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
तालिका विभिन्न स्कूलों से विभिन्न कक्षाओं में भाग लेने वाले छात्रों की संख्या को दर्शाता है।

7) दो छात्रों के एक समूह को स्कूल E से बनाना है ताकि समूह में खंड III में कम से कम एक छात्र हो। यह संभव हो सकने वाले तरीकों की संख्या 195 है। स्कूल E से पांच छात्रों की एक समूह बनाई जानी है, जिसमें खंड I के 2 छात्र, खंड II के 1 छात्र और खंड III के 2 छात्र शामिल हैं। उन तरीकों की संख्या ज्ञात करें जिनमें यह संभव हो सकता है?
a) 15920
b) 16478
c) 23420
d) 17820
e) इनमे से कोई नहीं
7) Answer: d)
स्कूल E से खंड III में छात्रों की संख्या= y
स्कूल E में छात्रों की कुल संख्या = (y + 12 + 18)
= y + 30
संभावित तरीकों की संख्या = yC1 * 30C1 + yC2 = 195
= > y * 30 + (y*(y-1)/(1 *2)) = 195
= > 30y + (y2 – y)/2 = 195
= > 60y + y2 – y = 390
= > y2 + 59y – 390 = 0
= > y2 + 65y – 6y – 390 = 0
= > y (y + 65) – 6 (y + 65) = 0
= > (y + 65) (y – 6) = 0
= > y = 6, -65 (ऋणात्मक मान को हटाने पर)
स्कूल E में छात्रों की कुल संख्या = 30 + 6 = 36
संभावित तरीकों की संख्या = 12C2 * 18C1 * 6C2
= (12*11/1*2) *18 *(6*5/1*2)
= 6*11*18*3*5
= 17820
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
तालिका विभिन्न स्कूलों से विभिन्न कक्षाओं में भाग लेने वाले छात्रों की संख्या को दर्शाता है।

8) स्कूल A में छात्रों की कुल संख्या ज्ञात कीजिये?
कथन I: स्कूल A से खंड II के सभी छात्र एक-दूसरे के साथ हैंडशेक कर रहे हैं और कुल हैंडशेक की संख्या 105 है।
कथन II: स्कूल A के सभी छात्र एक-दूसरे के साथ हैंडशेक कर रहे हैं और हैंडशेक की कुल संख्या 780 है।
a) केवल I
b) केवल II
c) I और II दोनों
d) या तो I या II
e) न तो I और न ही II
8) Answer: b)
I से,
स्कूल A से खंड II में छात्रों की संख्या= n
हैंडशेक की संख्या = nC2 = 105
= > [n*(n -1)] / (1 * 2) = 105
= > n2 – n = 210
= > n2 – n – 210 = 0
= > n2 – 15n + 14n – 210 = 0
= > n (n – 15) + 14 (n – 15) = 0
= > (n – 15) + (n – 14) = 0
= > n = 15, -14 (ऋणात्मक मान को हटाने पर)
कथन I से, हमें स्कूल A से खंड II में केवल छात्रों की संख्या का ज्ञात करना है। हम कुल छात्रों की संख्या नहीं ज्ञात कर सकते हैं।
इसलिए, दिए गए प्रश्न का उत्तर देने के लिए केवल कथन I पर्याप्त नहीं है।
II से,
स्कूल A से खंड II में छात्रों की संख्या= x
हैंडशेक की संख्या = xC2 = 780
= > x * (x – 1)/1*2 = 780
= > x2 – x = 780*2
= > x2 – x – 1560 = 0
= > x2 – 40x + 39x – 1560 = 0
= > x (x – 40) + 39 (x – 40) = 0
= > (x – 40) (x + 39) = 0
= > x = 40, -39 (ऋणात्मक मान को हटाने पर)
स्कूल A में छात्रों की कुल संख्या 40 है।
इसलिए, दिए गए प्रश्न का उत्तर देने के लिए केवल कथन II पर्याप्त है।
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
तालिका विभिन्न स्कूलों से विभिन्न कक्षाओं में भाग लेने वाले छात्रों की संख्या को दर्शाता है।

9) स्कूल B में, खंड III में छात्रों की संख्या खंड II में छात्रों की संख्या का 75% है।
मात्रा I: समिति P में, स्कूल B से पांच छात्रों का समूह बनाना है ताकि समूह में प्रत्येक खंड से 1 छात्र और किसी भी खंड से शेष छात्र शामिल हैं।
मात्रा II: समिति Q में, पांच छात्रों का समूह को स्कूल B से बनाना है, ताकि समिति में खंड I से कम से कम एक छात्र शामिल है।
a) मात्रा I > मात्रा II
b) मात्रा I < मात्रा II
c) मात्रा I ≥ मात्रा II
d) मात्रा I ≤ मात्रा II
e) मात्रा I = मात्रा II (या) संबंध निर्धारित नहीं किया जा सकता है
9) Answer: a)
स्कूल B से खंड II में छात्रों की संख्या= x
स्कूल B से खंड III में छात्रों की संख्या= 75/100 * x
= 3x / 4
स्कूल B से खंड II और III में छात्रों की कुल संख्या = 20 – 6 = 14
= > x + 3x/4 = 14
= > 7x/4 = 14
= > x = 8
स्कूल B से खंड III में छात्रों की संख्या = 8 * 75/100 = 6
मात्रा I:
तरीकों की संख्या = 6C1*8C1*6C1*(20-3)C2
= 6 * 8 * 6 *(17*16/1*2)
= 6*8*6*17*8
= 39168
मात्रा II: समिति Q में, पांच छात्रों का समूह को स्कूल B से बनाना है, ताकि समिति में खंड I से कम से कम एक छात्र शामिल है।
तरीकों की संख्या = 6C1*14C4 + 6C2*14C3 + 6C3*14C2 + 6C4*14C1 + 6C5
= 6006 + 5460 + 1820 + 210 + 6
= 13502
इसलिए, मात्रा I > मात्रा II
निर्देश (6 – 10): निम्नलिखित ग्राफ का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों के उत्तर दें।
तालिका विभिन्न स्कूलों से विभिन्न कक्षाओं में भाग लेने वाले छात्रों की संख्या को दर्शाता है।

10) प्रत्येक स्कूल B और स्कूल D से तीन सदस्यों की एक समिति बनाई जानी है। समिति के संभावित तरीकों की संख्या जिसमें स्कूल D से खंड III में तीन छात्र शामिल हैं समिति के संभावित तरीकों की संख्या जिसमें स्कूल B से खंड I में तीन छात्र शामिल हैं का कितना प्रतिशत हैं ?
a) 180%
b) 380%
c) 160%
d) 280%
e) इनमे से कोई नहीं
10) Answer: d)
स्कूल D में तरीकों की संख्या = 8C3
= 8*7*6/1*2*3
= 56
स्कूल B में तरीकों की संख्या = 6C3
= 6*5*4/1*2*3
= 20
आवश्यक प्रतिशत = 56/20 * 100 = 280%

