दिशा-निर्देश (प्रश्न 1 – 5): निम्नलिखित प्रश्नों में, दो समीकरण I और II दिए गए हैं। आपको दोनों समीकरणों को हल करना है और उत्तर देना है,
a) यदि x > y
b) यदि x ≥ y
c) यदि x < y
d) यदि x ≤ y
e) यदि x = y या संबंध स्थापित नहीं किया जा सकता है
1)
I) 2x2 + 19x + 45 = 0
II) y2 – 17y + 72 = 0
1) उत्तर: c)
I) 2x2 + 19x + 45 = 0
2x2 + 10x + 9x + 45 = 0
2x(x + 5) + 9 (x + 5) = 0
(2x + 9) (x + 5) = 0
x = -9/2, -5 = -4.5, -5
II) y2 – 17y + 72 = 0
(y – 8) (y – 9) = 0
y = 8, 9
x < y
दिशा-निर्देश (प्रश्न 1 – 5): निम्नलिखित प्रश्नों में, दो समीकरण I और II दिए गए हैं। आपको दोनों समीकरणों को हल करना है और उत्तर देना है,
a) यदि x > y
b) यदि x ≥ y
c) यदि x < y
d) यदि x ≤ y
e) यदि x = y या संबंध स्थापित नहीं किया जा सकता है
2)
I) 3x2 – 19x + 28 = 0
II) (256)1/4 y + (216)1/3 = 0
2) उत्तर: a)
I) 3x2 – 19x + 28 = 0
3x2 – 12x – 7x + 28 = 0
3x (x – 4) – 7 (x – 4) = 0
(x – 4) (3x – 7) = 0
x = 4, 7/3
II) (256)1/4 y = – (216)1/3
(44)1/4 y = – (63)1/3
4y = -6
y = – (6/4) = -1.5
x > y
दिशा-निर्देश (प्रश्न 1 – 5): निम्नलिखित प्रश्नों में, दो समीकरण I और II दिए गए हैं। आपको दोनों समीकरणों को हल करना है और उत्तर देना है,
a) यदि x > y
b) यदि x ≥ y
c) यदि x < y
d) यदि x ≤ y
e) यदि x = y या संबंध स्थापित नहीं किया जा सकता है
3)
I) 3/√x + 8/√x = √x
II) y2 = 95/2 / √y
3) उत्तर: a)
I) 3/√x + 8/√x = √x
11/√x = √x
11= x
II) y2 = 95/2/ √y
y2 × y1/2 = 95/2
y2 + (1/2) = 95/2
y5/2 = 95/2
y = 9
x > y
दिशा-निर्देश (प्रश्न 1 – 5): निम्नलिखित प्रश्नों में, दो समीकरण I और II दिए गए हैं। आपको दोनों समीकरणों को हल करना है और उत्तर देना है,
a) यदि x > y
b) यदि x ≥ y
c) यदि x < y
d) यदि x ≤ y
e) यदि x = y या संबंध स्थापित नहीं किया जा सकता है
4)
I) 2x2 +29x +50 =0
II) 12y2 – 7y +1 =0
4) उत्तर: c)
I) 2x2 +29x + 50 = 0
2x2 + 4x + 25x + 50 = 0
2x(x + 2) + 25(x + 2) = 0
(2x + 25) (x + 2) = 0
x = -25/2, -2
II) 12y2 – 7y +1 = 0
12y2 – 4y-3y +1 = 0
4y (3y – 1) -1(3y – 1) = 0
(4y-1) (3y-1) =0
y= ¼, 1/3
x < y
दिशा-निर्देश (प्रश्न 1 – 5): निम्नलिखित प्रश्नों में, दो समीकरण I और II दिए गए हैं। आपको दोनों समीकरणों को हल करना है और उत्तर देना है,
a) यदि x > y
b) यदि x ≥ y
c) यदि x < y
d) यदि x ≤ y
e) यदि x = y या संबंध स्थापित नहीं किया जा सकता है
5)
I) 5x2 + 23x +12 = 0
II) 15y2 +14y +3 = 0
5) उत्तर: d)
I) 5x2 + 23x + 12 = 0
5x2 + 20x + 3x + 12 = 0
5x(x + 4) + 3 (x + 4) = 0
(5x + 3) (x + 4) = 0
x = -3/5, -4
II) 15y2 +14y + 3 = 0
15y2 + 5y + 9y + 3 = 0
5y (3y + 1) + 3 (3y + 1) = 0
(5y + 3) (3y + 1) = 0
y= -3/5, -1/3
x ≤ y
दिशा-निर्देश (प्रश्न 6 – 10): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन कीजिये और दिए गए प्रश्नों के उत्तर दीजिये:
निम्न तालिका ठहरे हुए पानी में नाव की गति और धारा की गति और नाव द्वारा तय की गयी दूरी और स्थान तक पहुंचने के लिए गए समय को दर्शाती है। कुछ मान लुप्त हैं:
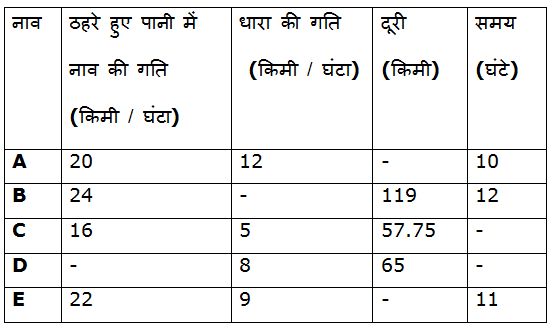
6) नाव A द्वारा तय की गयी दुरी और नाव B द्वारा तय की गयी दूरी के बीच का अंतर ज्ञात कीजिये?
a) 55 किमी
b) 62 किमी
c) 48 किमी
d) 69 किमी
e) इनमें से कोई नहीं
6) उत्तर: a)
धारा-अनुकूल की गति = ठहरे हुए पानी में नाव की गति + धारा की गति
=> 20 + 12 = 32 किमी / घंटा
धारा-प्रतिकूल की गति = ठहरे हुए पानी में नाव की गति – धारा की गति
=> 20 – 12 = 8 किमी / घंटा
समय = दूरी / गति
10 = (x/32) + (x/8)
10 = 40x/(32*8)
x = 64 किमी
नाव B द्वारा तय की गई दूरी = 119 किलोमीटर
आवश्यक अंतर = 119 – 64 = 55 किमी
(या)
दूरी = समय * [(ठहरे हुए पानी की गति2 – धारा की गति2 ) / (2 * ठहरे हुए पानी की गति)]
नाव A द्वारा तय की गई दूरी
=> 10 * [(202 – 122) / (2 * 20)] = 64 किमी
नाव B द्वारा तय की गई दूरी = 119 किलोमीटर
आवश्यक अंतर = 119 – 64 = 55 किमी
दिशा-निर्देश (प्रश्न 6 – 10): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन कीजिये और दिए गए प्रश्नों के उत्तर दीजिये:
निम्न तालिका ठहरे हुए पानी में नाव की गति और धारा की गति और नाव द्वारा तय की गयी दूरी और स्थान तक पहुंचने के लिए गए समय को दर्शाती है। कुछ मान लुप्त हैं:

7) उस स्थान तक पहुँचने के लिए नाव E से नाव C के द्वारा लिए गए समय के बीच का अनुपात ज्ञात कीजिये (धारा-अनुकूल और धारा-प्रतिकूल दोनों)?
a) 7: 11
b) 6: 11
c) 5: 11
d) 8: 11
e) इनमें से कोई नहीं
7) उत्तर: d)
ठहरे हुए पानी में नाव C की गति = 16 किमी / घंटा
धारा की गति (नाव C) = 5 किमी / घंटा
धारा-अनुकूल की गति = (16 + 5) = 21 किमी / घंटा
धारा-प्रतिकूल की गति = 16 – 5 = 11 किमी / घंटा
नाव C द्वारा स्थान तक पहुँचने में लिया गया समय
=> समय = (57.75 / 21) + (57.75 / 11)
=> 2.75 + 5.25 = 8 घंटा
नाव E द्वारा स्थान तक पहुँचने में लिया गया समय = 11 घंटा
आवश्यक अनुपात = 8: 11
दिशा-निर्देश (प्रश्न 6 – 10): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन कीजिये और दिए गए प्रश्नों के उत्तर दीजिये:
निम्न तालिका ठहरे हुए पानी में नाव की गति और धारा की गति और नाव द्वारा तय की गयी दूरी और स्थान तक पहुंचने के लिए गए समय को दर्शाती है। कुछ मान लुप्त हैं:

8) ठहरे हुए पानी में सभी दी गयी नावों की औसत गति को ज्ञात कीजिये, यदि नाव D द्वारा उस स्थान तक पहुंचने में लिया गया समय 9 घंटे है?
a) 24 किमी / घंटा
b) 20 किमी / घंटा
c) 18 किमी / घंटा
d) 16 किमी / घंटा
e) इनमें से कोई नहीं
8) उत्तर: b)
माना,ठहरे हुए पानी में नाव D की गति x है,
समय = दूरी / गति
9 = 65/(x + 8) + 65/(x – 8)
9 = [65x – 520 + 65x + 520]/[(x + 8) (x – 8)] [130x / (x2 – 64)] = 9
130x = 9x2 – 576
9x2 – 130x – 576 = 0
9x2 – 162x + 32x – 576 = 0
9x(x – 18) + 32(x – 18) = 0
(9x + 32) (x – 18) = 0
x = -32/9, 18 (ऋणात्मक मान को हटा दिया जाएगा)
ठहरे हुए पानी में सभी दी गयी नावों की औसत गति
= > (20 + 24 + 16 + 18 + 22)/5 = 100/5
= > 20 किमी / घंटा
दिशा-निर्देश (प्रश्न 6 – 10): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन कीजिये और दिए गए प्रश्नों के उत्तर दीजिये:
निम्न तालिका ठहरे हुए पानी में नाव की गति और धारा की गति और नाव द्वारा तय की गयी दूरी और स्थान तक पहुंचने के लिए गए समय को दर्शाती है। कुछ मान लुप्त हैं:

9) सभी दी गई नावों में धारा की गति का योग, ठहरे हुए पानी में सभी दी गई नावों की गति के योग का लगभग कितना प्रतिशत है, यदि नाव D द्वारा उस स्थान तक पहुँचने में लिया गया समय 9 घंटे है?
a) 52 %
b) 58 %
c) 44 %
d) 65 %
e) इनमे से कोई नहीं
9) उत्तर: c)
माना,नाव B में धारा की गति x है,
= > 12 = [119/(24 + x) + 119/(24 – x)]
= > 12 = (2856 – 119x + 2856 + 119x) / (24 + x) (24 – x)
= > 12 = [5712 / (576 – x2)
= > 12*(576 – x2) = 5712
= > 6912 – 12x2 = 5712
= > 1200 = 12x2
= > x2 = 100
= > x = 10, -10 (ऋणात्मक मान को हटा दिया जाएगा)
तो, नाव B में धारा की गति = 10 किमी / घंटा
सभी दी गई नावों में धारा की गति का योग
= > 12 + 10 + 5 + 8 + 9 = 44 किमी / घंटा
माना,ठहरे हुए पानी में नाव D की गति y है,
समय = दूरी / गति
9 = 65/(y + 8) + 65/(y – 8)
9 = [65y – 520 + 65y + 520]/[(y + 8) (y – 8)] [130y / (y2 – 64)] = 9
130y = 9y2 – 576
9y2 – 130y – 576 = 0
9y2 – 162y + 32y – 576 = 0
9y (y – 18) + 32(y – 18) = 0
(9y + 32) (y – 18) = 0
y = -32/9, 18 (ऋणात्मक मान को हटा दिया जाएगा)
इसीलिए, ठहरे हुए पानी में नाव D की गति = 18 किमी / घंटा
ठहरे हुए पानी में सभी दी गयी नावों की गति का योग
= > 20 + 24 + 16 + 18 + 22 = 100 किमी / घंटा
आवश्यक%= (44/100)*100 = 44 %
दिशा-निर्देश (प्रश्न 6 – 10): निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन कीजिये और दिए गए प्रश्नों के उत्तर दीजिये:
निम्न तालिका ठहरे हुए पानी में नाव की गति और धारा की गति और नाव द्वारा तय की गयी दूरी और स्थान तक पहुंचने के लिए गए समय को दर्शाती है। कुछ मान लुप्त हैं:

10) नाव E द्वारा तय की गई दूरी को ज्ञात कीजिए?
a) 92.25 किमी
b) 86.5 किमी
c) 106.25 किमी
d) 100.75 किमी
e) इनमें से कोई नहीं
10) उत्तर: d)
दूरी = समय * [(ठहरे हुए पानी की गति2 – धारा की गति2 ) / (2 * ठहरे हुए पानी की गति)]
नाव A द्वारा तय की गई दूरी
= > 11*[(222 – 92)/(2*22)]
= > 11*[(484 – 81)/44] = 100.75 किमी

