1) कार्तिक की कुल वार्षिक आय 360000 रूपये है। वह अपने बेटे की शिक्षा के लिए अपनी मासिक आय का 25% खर्च करता है, शेष आय का 30% अपने घर के खर्चों के लिए और शेष बचा लेता है, तो फिर एक वर्ष में कितनी बचत कर पाता है?
a) 172500 रूपये
b) 196400 रूपये
c) 167800 रूपये
d) 189000 रूपये
e) इनमे से कोइ नहीं
1) उत्तर: d)
वेतन प्रति माह = 360000/12 = 30000 रु
प्रश्न के अनुसार,
प्रति माह बचत = 30000 * (75/100) * (70/100) = 15750
एक साल में बचत = 15750*12 = 189000 रूपये
2) A, B और C ने 5:8:10 के अनुपात में निवेश करके व्यवसाय शुरू किया। यदि 20% लाभ चैरिटी में जाता है, तो शेष तीनों द्वारा साझा किया जाएगा। B का हिस्सा 40000 रूपये है। कुल लाभ ज्ञात कीजिये?
a) 143750 रूपये
b) 156250 रूपये
c) 128500 रूपये
d) 134800 रूपये
e) इनमे से कोइ नहीं
2) उत्तर: a)
निवेश अनुपात = 5 : 8 : 10
B का हिस्सा = 40000
8 का = 40000
1 का = 5000
23 का = 5000*23 = 115000
80 % का कुल लाभ = 115000
(80/100) * कुल लाभ = 115000
कुल लाभ = 115000*(100/80) = 143750 रूपये
3) 7 वर्षों के लिए एक निश्चित राशि पर साधारण ब्याज राशि का (14/25) है। ब्याज दर ज्ञात कीजिये?
a) 12 %
b) 10 %
c) 8 %
d) 14 %
e) इनमे से कोइ नहीं
3) उत्तर: c)
साधारण ब्याज = P*n*r /100
(14/25) * P = P * 7 * r/100
ब्याज की दर (r) = (14/25) * (100/7)
r = 8 %
4) सात साल पहले, कार्तिका की उम्र और सानू की वर्तमान आयु 3: 4 के अनुपात में है। आठ साल बाद, कार्तिका और सानू की आयु 15: 14 के अनुपात में होगी| सानू की वर्तमान उम्र ज्ञात कीजिये?
a) 16 वर्ष
b) 20 वर्ष
c) 24 वर्ष
d) 28 वर्ष
e) इनमे से कोइ नहीं
4) उत्तर: b)
कार्तिका की आयु का अनुपात, 7 वर्ष पहले और सानू की वर्तमान आयु
= 3: 4 (3x, 4x)
कार्तिका और सानू की वर्तमान आयु = 3x + 7, 4x
प्रश्न के अनुसार,
(3x + 7 + 8)/(4x + 8) = (15/14)
42x + 210 = 60x + 120
90 = 18x
X = 90/18 = 5
सानू की वर्तमान आयु = 4x = 20 वर्ष
5) एक बॉक्स में 4 लाल गेंद, 3 सफेद गेंद, 2 काली गेंद और 5 गुलाबी गेंद होती हैं। कम से कम एक गुलाबी गेंद प्राप्त करने की संभावना ज्ञात कीजिये, यदि चार गेंदों को यादृच्छिक रूप से निकाला जाता है?
a) 75/152
b) 89/127
c) 125/143
d) 172/255
e) इनमे से कोइ नहीं
5) उत्तर: c)
P(E) = n(E)/n(S)
n(S) = 14C4
कम से कम एक गुलाबी गेंद प्राप्त करने की संभावना,
आवश्यक संभावना = 1 – कोई भी गुलाबी गेंद नहीं है
P (कोई भी गुलाबी गेंद नहीं है) = 9C4
P(E) = 9C4/ 14C4
P(E) = 18/143
आवश्यक संभावना = 1 – (18/143) = 125/143
निर्देश (Q. 6 – 10) निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों को उत्तर दें:
निम्नलिखित पाई चार्ट विभिन्न स्कूलों से प्रतिभा परीक्षा में भाग लेने वाले कुल छात्रों के प्रतिशत वितरण को दर्शाता है।
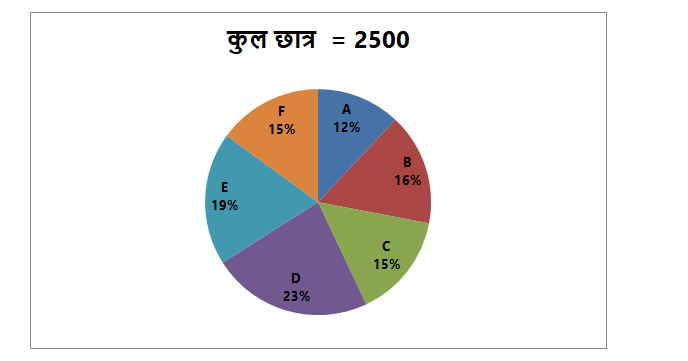
6) स्कूल A और स्कूल B में पढ़ने वाले छात्रों की कुल संख्या के बीच का अंतर क्या है, अगर स्कूल A और B की प्रतिभा परीक्षा में शामिल नहीं होने वाले कुल छात्रों का प्रतिशत क्रमशः 85% और 84% है?
a) 360
b) 540
c) 500
d) 450
e) इनमे से कोइ नहीं
6) उत्तर: c)
स्कूल A में पढ़ने वाले छात्रों की कुल संख्या
=> 2500 * (12/100) * (100/15) = 2000
स्कूल B में पढ़ने वाले छात्रों की कुल संख्या
=> 2500 * (16/100) * (100/16) = 2500
आवश्यक अंतर = 2500 – 2000 = 500
निर्देश (Q. 6 – 10) निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों को उत्तर दें:
निम्नलिखित पाई चार्ट विभिन्न स्कूलों से प्रतिभा परीक्षा में भाग लेने वाले कुल छात्रों के प्रतिशत वितरण को दर्शाता है।

7) स्कूल D और F से प्रतिभा की परीक्षा में भाग लेने वाली महिला छात्रों की कुल संख्या के बीच अनुपात ज्ञात कीजिये, यदि स्कूल D और F से प्रतिभा परीक्षा में भाग लेने वाली महिला छात्रों की कुल संख्या के बीच अनुपात क्रमशः 3: 2 और 7: 8 है?
a) 52 : 43
b) 47 : 35
c) 15 : 7
d) 23 : 12
e) इनमे से कोइ नहीं
7) उत्तर: a)
स्कूल D और F से एक साथ प्रतिभा परीक्षा में भाग लेने वाले कुल छात्रों की कुल संख्या
=> 2500 * (23/100) * (3/5) + 2500 * (15/100) * (7/15)
=> 345 + 175 = 520
स्कूल D और F से एक साथ प्रतिभा परीक्षा में भाग लेने वाली कुल महिला छात्र
=> 2500 * (23/100) * (2/5) + 2500 * (15/100) * (8/15)
=> 230 + 200 = 430
आवश्यक अनुपात = 520 : 430 = 52 : 43
निर्देश (Q. 6 – 10) निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों को उत्तर दें:
निम्नलिखित पाई चार्ट विभिन्न स्कूलों से प्रतिभा परीक्षा में भाग लेने वाले कुल छात्रों के प्रतिशत वितरण को दर्शाता है।

8) स्कूल C, D और E से एक साथ प्रतिभा परीक्षा में भाग लेने वाले छात्रों की औसत संख्या ज्ञात कीजिए?
a) 420
b) 475
c) 445
d) 490
e) इनमे से कोइ नहीं
8) उत्तर: b)
स्कूल C, D और E से एक साथ प्रतिभा परीक्षा में भाग लेने वाले छात्रों की औसत संख्या
= > 2500*[(15 + 23 + 19)/100]*(1/3) = 475
निर्देश (Q. 6 – 10) निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों को उत्तर दें:
निम्नलिखित पाई चार्ट विभिन्न स्कूलों से प्रतिभा परीक्षा में भाग लेने वाले कुल छात्रों के प्रतिशत वितरण को दर्शाता है।

9) स्कूल A और B से एक साथ प्रतिभा परीक्षा में शामिल होने वाले छात्रों की कुल संख्या, स्कूल E में पढ़ने वाले छात्रों की कुल संख्या का लगभग कितना प्रतिशत है, यदि स्कूल E से प्रतिभा परीक्षा में भाग लेने वाले छात्रों का प्रतिशत 25% है?
a) 48 %
b) 55 %
c) 64 %
d) 37 %
e) 72 %
9) उत्तर: d)
स्कूल A और B से एक साथ प्रतिभा परीक्षा में शामिल होने वाले छात्रों की कुल संख्या
=> 2500 * (28/100) = 700
स्कूल E में पढ़ने वाले छात्रों की कुल संख्या
=> 2500 * (19/100) * (100/25) = 1900
अपेक्षित % = (700/1900)*100 = 36.84 % = 37 %
निर्देश (Q. 6 – 10) निम्नलिखित जानकारी का ध्यानपूर्वक अध्ययन करें और दिए गए प्रश्नों को उत्तर दें:
निम्नलिखित पाई चार्ट विभिन्न स्कूलों से प्रतिभा परीक्षा में भाग लेने वाले कुल छात्रों के प्रतिशत वितरण को दर्शाता है।

10) स्कूल A और C और स्कूल B और D से एक साथ प्रतिभा परीक्षा में भाग लेने वाले छात्रों की औसत संख्या के बीच अंतर ज्ञात कीजिये?
a) 180
b) 200
c) 150
d) 120
e) इनमे से कोइ नहीं
10) उत्तर: c)
स्कूल A और C से एक साथ प्रतिभा परीक्षा में भाग लेने वाले छात्रों की औसत संख्या
=> 2500 * (27/100) * (1/2)
स्कूल B और D से एक साथ प्रतिभा परीक्षा में भाग लेने वाले छात्रों की औसत संख्या
=> 2500 * (39/100) * (1/2)
आवश्यक अंतर = (2500/200) * (39 – 27) = (25/2) * 12 = 150

