निर्देश (1 – 5): निम्नलिखित आंकड़ों का ध्यानपूर्वक अध्ययन करें और प्रश्नों के उत्तर दें:
नीचे दिए गए पाई चार्ट में P, Q, R, S और T सहित पांच वस्तुओं के क्रय मूल्य के प्रतिशत वितरण को दर्शाया गया है।
पाई चार्ट का योग 36000 रुपये है।
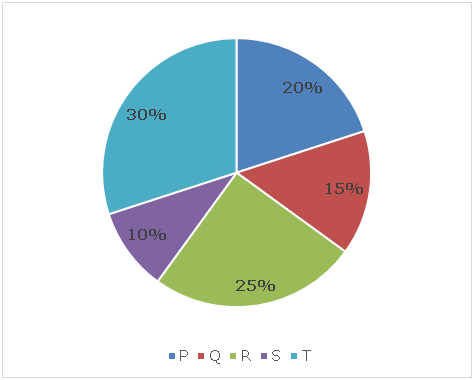
नीचे दिये गये बार ग्राफ में उन पाँच वस्तुओं के अंकित मूल्य पर दुकानदार A और दुकानदार B द्वारा दी गई छूट के प्रतिशत को दर्शाया गया है।
नोट: यह आवश्यक नहीं है कि किसी वस्तु का अंकित मूल्य दोनों दुकानदारों के लिए समान हो।
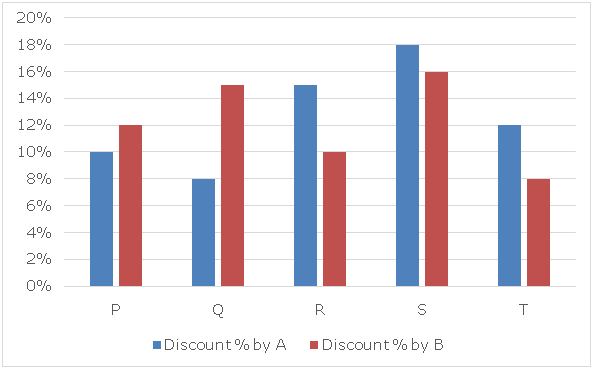
1) यदि दुकानदार A की वस्तुएं P और Q पर अंकित मूल्य क्रमशः 35% और 15% है और उसने इन वस्तुओं को क्रमशः ‘x’% और ‘y’% के लाभ पर बेचा है, तो ‘x’ के मान और ‘y’ के मान में क्या अंतर है?
a) 14.8
b) 15.7
c) 15.4
d) 13.5
e) इनमें से कोई नहीं
निर्देश (1 – 5):
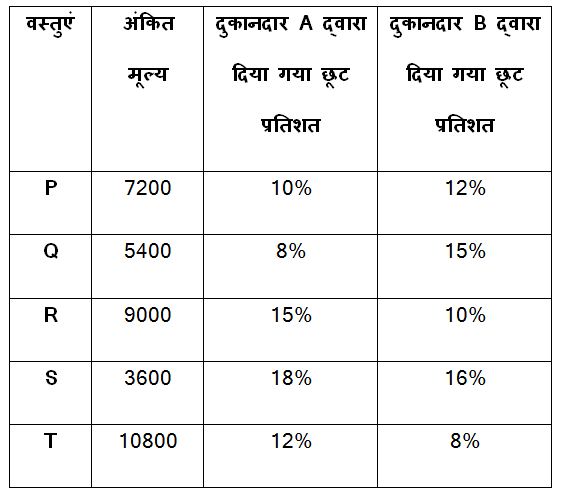
वस्तु P का क्रय मूल्य = 36000 का 20% = 7200 रुपये
वस्तु Q का क्रय मूल्य = 36000 का 15% = 5400 रुपये
वस्तु R का क्रय मूल्य = 36000 का 25% = 9000 रुपये
वस्तु S का क्रय मूल्य = 36000 का 10% = 3600 रुपये
वस्तु T का क्रय मूल्य = 36000 का 30% = 10800 रुपये
1) उत्तर : b)
दुकानदार A के लिए वस्तु P पर अंकित मूल्य = 7200 का 135% = 9720 रुपये
दुकानदार A के लिए वस्तु P का विक्रय मूल्य = 9720 का 90% = 8748 रुपये
दुकानदार A द्वारा वस्तु P पर अर्जित लाभ = 8748 – 7200 = 1548 रुपये
दुकानदार A के लिए वस्तु Q पर अंकित मूल्य = 5400 का 115% = 6210 रुपये
दुकानदार A के लिए वस्तु Q का विक्रय मूल्य = 6210 का 92% = 5713.2 रुपये
दुकानदार A द्वारा वस्तु Q पर अर्जित लाभ = 5713.2 – 5400 = 313.2 रुपये
प्रश्न के अनुसार:
x% = (1548/7200) * 100
x% = 21.5%
x = 21.5
y% = (313.2/5400) * 100
y% = 5.8%
y = 5.8
अंतर = x ~ y = 21.5 – 5.8 = 15.7
2) दुकानदार A ने वस्तु P के अंकित मूल्य को इसके क्रय मूल्य से ‘x’% अधिक अंकित किया और यह वस्तु ‘x – 13’% पर बेच दी, जबकि दुकानदार B ने वस्तु P के अंकित मूल्य को इसके क्रय मूल्य से ‘y’% अधिक अंकित किया और यह वस्तु ‘y – 15’% पर बेच दी, तो वस्तु P को बेचने के बाद दोनों दुकानदारों को प्राप्त लाभ का योग क्या है?
a) 1260 रुपये
b) 1520 रुपये
c) 1390 रुपये
d) 1944 रुपये
e) इनमें से कोई नहीं
2) उत्तर : d)
दुकानदार A के लिए वस्तु P पर अंकित मूल्य = 7200 का (100 + x)% = 72(100 + x)
दुकानदार A के लिए वस्तु P का विक्रय मूल्य = 72(100 + x) का 90%
दिया गया है, 72(100 + x) का 90% = 7200 का (100 + x – 13)%
64.8(100 + x) = 72(87 + x)
0.9(100 + x) = (87 + x)
90 + 0.9x = 87 + x
3 = 0.1x
x = 30
वस्तु P को बेचने के बाद दुकानदार A द्वारा अर्जित लाभ = 7200 का (x – 13)% = 7200 का 17% = 1224 रुपये
दुकानदार B के लिए वस्तु P पर अंकित मूल्य = 7200 का (100 + y)% = 72(100 + y)
दुकानदार B के लिए वस्तु P का विक्रय मूल्य = 72(100 + y) का 88%
दिया गया है, 72(100 + y) का 88% = 7200 का (100 + y – 15)%
63.36(100 + y) = 72(85 + y)
0.88(100 + y) = 85 + y
88 + 0.88y = 85 + y
3 = 0.12y
y = 25
वस्तु P को बेचने के बाद दुकानदार B द्वारा अर्जित लाभ = 7200 का (y – 15)% = 7200 का 10% = 720 रुपये
वस्तु P को बेचने के बाद दोनों दुकानदारों द्वारा अर्जित लाभ का योग = 1224 + 720 = 1944 रुपये
3) दुकानदार A द्वारा वस्तु Q पर अंकित मूल्य दुकानदार B द्वारा अंकित मूल्य का आधा है और वस्तु Q को बेचने के बाद दोनों दुकानदारों को अर्जित लाभ राशि का योग 330 रुपये है, तो दुकानदार A और दुकानदार B द्वारा वस्तु Q को बेचने के लिए दी गई छूट का अनुपात क्या है?
a) 7: 13
b) 16: 33
c) 15: 8
d) 26: 63
e) इनमें से कोई नहीं
3) उत्तर : b)
माना दुकानदारों A और B द्वारा वस्तु Q पर अंकित मूल्य क्रमशः x और 2x है।
दुकानदार A के लिए वस्तु Q का अंकित मूल्य = (5400 + x)
दुकानदार A के लिए वस्तु Q का विक्रय मूल्य = (5400 + x) का 92% = (4968 + 0.92x)
लाभ राशि = (4968 + 0.92x) – 5400 = (0.92x – 432)
दुकानदार B के लिए वस्तु Q का अंकित मूल्य = (5400 + 2x)
दुकानदार B के लिए वस्तु Q का विक्रय मूल्य = (5400 + 2x) का 85% = (4590 + 1.7x)
लाभ राशि = (4590 + 1.7x) – 5400 = (1.7x – 810)
प्रश्न के अनुसार:
(0.92x – 432) + (1.7x – 810) = 330
2.62x – 1242 = 330
2.62x = 1572
x = 600
दुकानदार A द्वारा दी गई छूट = (5400 + x) का 8% = 480 रुपये
दुकानदार B द्वारा दी गई छूट = (5400 + 2x) का 15% = 990 रुपये
अनुपात = 480: 990 = 16: 33
4) यदि वस्तु T के लिए दुकानदार A और दुकानदार B के अंकित मूल्य का अनुपात 7: 6 है और दुकानदार A द्वारा दी जाने वाली छूट की राशि दुकानदार B की तुलना में 648 रुपये अधिक है, तो वस्तु T को बेचने के बाद दोनों दुकानदारों को प्राप्त लाभ का अनुमानित प्रतिशत क्या है?
a) 44.88%
b) 66.66%
c) 33.33%
d) 55.55%
e) 28.82%
4) उत्तर : a)
माना दुकानदारों A और B द्वारा वस्तु T पर अंकित मूल्य क्रमशः 7x और 6x है।
दुकानदार A के लिए वस्तु T का अंकित मूल्य = (10800 + 7x)
दुकानदार A द्वारा दी गई छूट = (10800 + 7x) का 12% = (1296 + 0.84x)
दुकानदार B के लिए वस्तु T का अंकित मूल्य = (10800 + 6x)
दुकानदार B द्वारा दी गई छूट = (10800 + 6x) का 8% = (864 + 0.48x)
प्रश्न के अनुसार:
(1296 + 0.84x) – (864 + 0.48x) = 648
432 + 0.36x = 648
0.36x = 216
x = 600
दुकानदार A को अर्जित लाभ = [88% of (10800 + 7x)] – 10800
= 2400 रुपये
दुकानदार B को अर्जित लाभ = [92% of (10800 + 6x)] – 10800
= 2448 रुपये
लाभ प्रतिशत = [(2400 + 2448)/10800] * 100 = 44.88%
5) दुकानदार B ने एक ग्राहक को R और S दो वस्तुएं बेचीं, लेकिन उसने एक संचित छूट की बजाय दोनों वस्तुओं पर लगातार दो छूट दीं। वस्तु R पर क्रमशः 5% और 20% छूट दी, जबकि वस्तु S पर क्रमशः 220 रुपये और 15% छूट दी और वस्तु R और S पर अंकित प्रतिशत क्रमशः 40% और 45% है, तो दोनों वस्तुओं को बेचने के बाद दुकानदार को कुल लाभ कितना होगा?
a) 1264 रुपये
b) 1148 रुपये
c) 1226 रुपये
d) 1072 रुपये
e) इनमें से कोई नहीं
5) उत्तर : c)
वस्तु R का अंकित मूल्य = 9000 का 140% = 12600 रुपये
लगातार दो छूट के बाद वस्तु R का विक्रय मूल्य = 12600 का 80% का 95%
= 9576 रुपये
वस्तु S का अंकित मूल्य = 3600 का 145% = 5220 रुपये
लगातार दो छूट के बाद वस्तु S का विक्रय मूल्य = (5220 – 220) का 85%
= 4250 रुपये
दुकानदार द्वारा अर्जित कुल लाभ
= (9576 + 4250) – (9000 + 3600) = 1226 रुपये
निर्देश (6 – 10): निम्नलिखित आंकड़ों का ध्यानपूर्वक अध्ययन करें और प्रश्नों के उत्तर दें:
एक राज्य में A और B दो शहर हैं। एक पक्षी सोमवार से शुक्रवार तक सप्ताह के पांच अलग-अलग दिनों में अपने भोजन के लिए सुबह शहर A से शहर B तक उड़ान भरता है और शाम को शहर A में वापस आ जाता है।
नोट 1: सुबह शहर A से शहर B तक पक्षी के उड़ने की गति (हवा के बिना) सभी पांच दिनों में अलग-अलग होती है, जबकि शाम को शहर B से शहर A तक पक्षी के उड़ने की गति (हवा के बिना) भी सभी दिन अलग-अलग होती है।
2: हवा की दिशा समान रहती है और यह शहर B से शहर A की तरफ रहती है। सुबह में हवा की गति 50 किमी / घंटा रहती है, जबकि शाम को हवा की गति 40 किमी / घंटा रहती है।
नीचे दिये गये पहले पाई चार्ट में सभी पांचों दिनों में सुबह में शहर A से शहर B तक पक्षी के उड़ने की गति (हवा के बिना) के प्रतिशत का वितरण दर्शाया गया है और पाई चार्ट का योग 1000 किमी / घंटा है।
नीचे दिये गये दुसरे पाई चार्ट में सभी पांचों दिनों में शाम में शहर B से शहर A तक पक्षी के उड़ने की गति (हवा के बिना) के प्रतिशत का वितरण दर्शाया गया है और पाई चार्ट का योग 800 किमी / घंटा है।

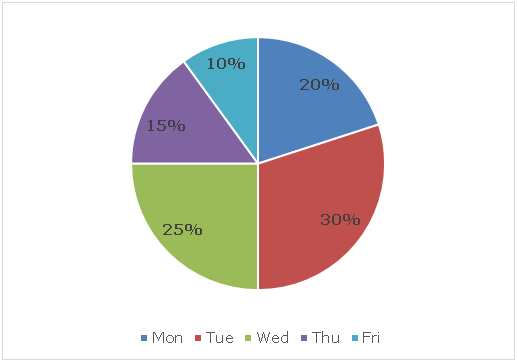
6) यदि शहर A और शहर B के बीच की दूरी 270 किमी है, तो सोमवार की सुबह शहर A से शहर B तक पहुंचने में पक्षी द्वारा लिए गए समय और शुक्रवार की शाम को शहर B से शहर A तक पहुंचने में पक्षी को लगने वाले समय में क्या अंतर है?
a) 36 मिनट
b) 18 मिनट
c) 45 मिनट
d) 27 मिनट
e) इनमें से कोई नहीं
निर्देश (6 – 10):
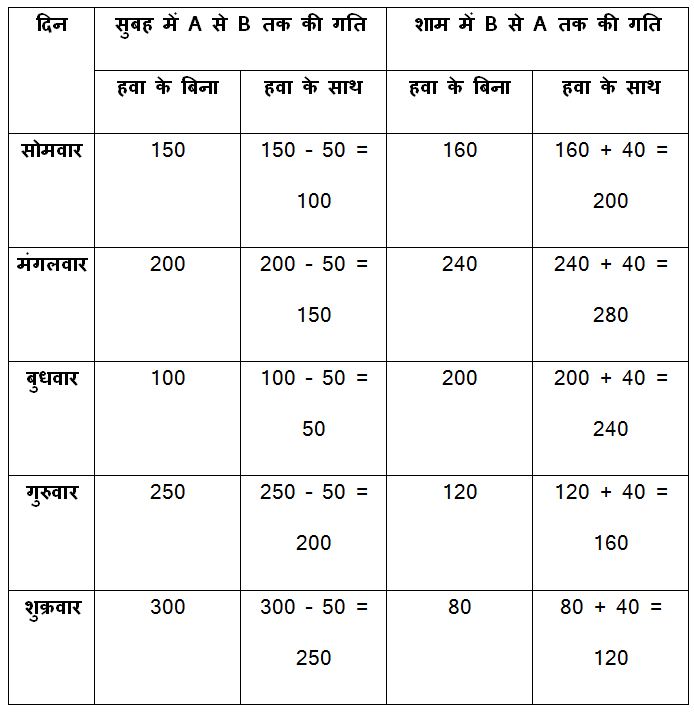
सोमवार सुबह शहर A से शहर B तक पक्षी के उड़ने की गति (हवा के बिना) = 1000 का 15%
= 150 किमी/घंटा
मंगलवार को शहर A से शहर B तक पक्षी के उड़ने की गति (हवा के बिना) = 1000 का 20%
= 200 किमी/घंटा
बुधवार को शहर A से शहर B तक पक्षी के उड़ने की गति (हवा के बिना) = 1000 का 10%
= 100 किमी/घंटा
गुरूवार को शहर A से शहर B तक पक्षी के उड़ने की गति (हवा के बिना) = 1000 का 25%
= 250 किमी/घंटा
शुक्रवार को शहर A से शहर B तक पक्षी के उड़ने की गति (हवा के बिना) = 1000 का 30%
= 300 किमी/घंटा
सोमवार को शहर B से शहर A तक पक्षी के उड़ने की गति (हवा के बिना) = 800 का 20%
= 160 किमी/घंटा
मंगलवार को शहर B से शहर A तक पक्षी के उड़ने की गति (हवा के बिना) = 800 का 30%
= 240 किमी/घंटा
बुधवार को शहर B से शहर A तक पक्षी के उड़ने की गति (हवा के बिना) = 800 का 25%
= 200 किमी/घंटा
गुरुवार को शहर B से शहर A तक पक्षी के उड़ने की गति (हवा के बिना) = 800 का 15%
= 120 किमी/घंटा
शुक्रवार को शहर B से शहर A तक पक्षी के उड़ने की गति (हवा के बिना) = 800 का 10%
= 80 किमी/घंटा
6) उत्तर : d)
शहर A और B के बीच की दूरी = 270 किमी
सोमवार सुबह में शहर A से शहर B तक पहुंचने में पक्षी द्वारा लिया गया समय
= 270/100 = 2.7 घंटे
शुक्रवार शाम में शहर B से शहर A तक पहुंचने में पक्षी द्वारा लिया गया समय
= 270/120 = 2.25 घंटे
अंतर = 2.7 – 2.25 = 0.45 hours = 27 मिनट
7) बुधवार की सुबह पक्षी शहर A से शहर B की ओर उड़ना शुरू करता है और उसी समय एक अन्य पक्षी 120 किमी/घंटे (हवा के बिना) की गति से शहर B से शहर A की ओर उड़ता है। यदि दोनों पक्षियों के आपस में मिलने से पहले उनके द्वारा तय की गई कुल दूरी के बीच 90 किमी का अंतर है, तो A और B शहरों के बीच की दूरी क्या है?
a) 110 किमी
b) 220 किमी
c) 165 किमी
d) 198 किमी
e) इनमें से कोई नहीं
7) उत्तर : c)
बुधवार की सुबह हवा के बिना अन्य पक्षी के उड़ने की गति = 120 किमी/घंटा
बुधवार की सुबह हवा के साथ अन्य पक्षी के उड़ने की गति = 120 + 50
= 170 किमी/घंटा
दोनों पक्षियों की प्रभावी गति = 50 + 170 = 220 किमी/घंटा
माना दोनों पक्षी ‘t’ घंटे की यात्रा के बाद मिलेंगे
अंतर = 170t – 50t = 90
120t = 90
t = 0.75 घंटे
दोनों शहरों के बीच की दूरी = 220 * 0.75 = 165 किमी
8) यदि पक्षी शुक्रवार को सुबह 6:00 बजे शहर A से शहर B की ओर उड़ान भरना शुरू कर देता है और शहर में भोजन की तलाश करता है। भोजन खोजने की प्रक्रिया में वह 7 घंटे 9 मिनट वहां बिताता है और उसी दिन शाम को 3:00 बजे शहर A में वापस आ जाता है, तो फिर शहर A से शहर B कितनी दूर है? मान लें कि उड़ान और भोजन की खोज के अलावा समय का और कहीं कोई नुकसान नहीं हुआ है।
a) 150 किमी
b) 120 किमी
c) 180 किमी
d) 135 किमी
e) इनमें से कोई नहीं
8) उत्तर : a)
उसी दिन सुबह 6 से शाम 3 बजे के बीच का समय
= 9 घंटे = 540 मिनट
खाना खोजने में लगा समय = 7 घंटे 9 मिनट = (7 * 60) + 9 = 429 मिनट
उड़ान में लगा समय = 540 – 429 = 111 मिनट
मना शहर A से शहर B के बीच की दूरी ‘D’ किमी है।
प्रश्न के अनुसार:
(D/250) + (D/120) = (111/60)
(12D + 25D)/3000 = 111/60
37D = (111/60) * 3000
37D = 5550
D = 150
अत:, शहर A से शहर B के बीच की दूरी 150 किमी है।
9) यदि शहरों A और B के बीच की दूरी 98 किमी है और मंगलवार की शाम को हवा की गति 20 किमी / घंटा बढ़ जाती है और पक्षी भी शहर B से A की ओर लौटते समय अपनी उड़ान (बिना हवा के) की गति बढ़ा देता है, तो पक्षी द्वारा शहर B से A तक पहुंचने में लिया गया समय पक्षी द्वारा लिये जाने वाले समय की तुलना में 4.2 मिनट कम होता है, तो फिर पक्षी के उड़ने (बिना हवा के) की गति में कितनी वृद्धि होती है?
a) 40 किमी/घंटा
b) 50 किमी/घंटा
c) 25 किमी/घंटा
d) 35 किमी/घंटा
e) इनमें से कोई नहीं
9) उत्तर : b)
माना पक्षी की उड़ान की गति में वृद्धि = ‘x’ किमी/घंटा
मंगलवार शाम को शहर B से A में लौटते समय पक्षी की प्रभावी गति = (280 + 20 + x) = (300 + x) किमी/घंटा
पक्षी द्वारा लिया जाने वाला समय = (98/280) * 60 = 21 मिनट
पक्षी द्वारा लिया गया वास्तविक समय = (21 – 4.2) = (98 * 60)/(300 + x)
300 + x = 350
x = 50
पक्षी के उड़ने की गति में वृद्धि (हवा के बिना) = x = 50 किमी/घंटा
10) यदि गुरुवार की सुबह पक्षी शहर A से शहर B तक उड़ान भरता है, लेकिन उसके उड़ने की गति (हवा के बिना) अपनी मूल उड़ान (हवा के बिना) गति से 20% अधिक है और वह उसी दिन शाम को चार्ट में उल्लेखित हवा की गति के साथ अपने मूल बिंदु पर वापस आता है। अगर शहरों A और B के बीच की दूरी 80 किमी है, तो पक्षी की उड़ान में अपने मूल समय से कितना कम समय लगेगा?
a) 3.2 मिनट
b) 5.4 मिनट
c) 4.8 मिनट
d) 3.6 मिनट
e) इनमें से कोई नहीं
10) उत्तर : c)
बदली हुई पक्षी के उड़ने की गति (हवा के बिना) = 250 का 120% = 300 किमी/घंटा
बदली हुई पक्षी के उड़ने की गति (हवा के साथ) = 300 – 50 = 250 किमी/घंटा
पक्षी की उड़ान का मूल समय = (80/200) + (80/160) = 0.4 + 0.5 = 0.9 घंटे
= 54 मिनट
पक्षी की उड़ान का मूल समय = (80/250) + (80/160) = 0.32 + 0.5 = 0.82 घंटे
= 49.2 मिनट
कम समय = 54 – 49.2 = 4.8 मिनट

